Specifying models using model builder¶
Since the scope of Treelite is limited to prediction only, one must use other machine learning packages to train decision tree ensemble models. In this document, we will show how to import an ensemble model that had been trained elsewhere.
Using XGBoost or LightGBM for training? Read this document instead.
Contents
What is the model builder?¶
The ModelBuilder class is a tool used to specify decision
tree ensembles programmatically. Each tree ensemble is represented as follows:
Each
Treeobject is a dictionary of nodes indexed by unique integer keys.A node is either a leaf node or a test node. A test node specifies its left and right children by their integer keys in the tree dictionary.
Each
ModelBuilderobject is a list ofTreeobjects.
A toy example¶
Consider the following tree ensemble, consisting of two regression trees:
Note
Provision for missing data: default directions
Decision trees in treelite accomodate missing data by indicating the default direction for every test node. In the diagram above, the default direction is indicated by label “Missing.” For instance, the root node of the first tree shown above will send to the left all data points that lack values for feature 0.
For now, let’s assume that we’ve somehow found optimal choices of default directions at training time. For detailed instructions for actually deciding default directions, see Section 3.4 of the XGBoost paper.
Let us construct this ensemble using the model builder. First step is to assign unique integer key to each node. In the following diagram, integer keys are indicated in red. Note that integer keys need to be unique only within the same tree.
Next, we create a model builder object by calling the constructor for
ModelBuilder, with an num_feature argument indicating
the total number of features used in the ensemble:
import treelite
builder = treelite.ModelBuilder(num_feature=3)
We also create a tree object; it will represent the first tree in the ensemble.
# to represent the first tree
tree = treelite.ModelBuilder.Tree()
The first tree has five nodes, each of which is to be inserted into the tree one at a time. The syntax for node insertion is as follows:
tree[0] # insert a new node with key 0
Once a node has been inserted, we can refer to it by writing
tree[0] # refer to existing node #0
The meaning of the expression tree[0] thus depends on whether the node #0
exists in the tree or not.
We may combine node insertion with a function call to specify its content.
For instance, node #0 is a test node, so we call
set_numerical_test_node():
# Node #0: feature 0 < 5.0 ? (default direction left)
tree[0].set_numerical_test_node(feature_id=0,
opname='<',
threshold=5.0,
default_left=True,
left_child_key=1,
right_child_key=2)
On the other hand, node #2 is a leaf node, so call
set_leaf_node() instead:
# Node #2: leaf with output +0.6
tree[2].set_leaf_node(0.6)
Let’s go ahead and specify the other three nodes:
# Node #1: feature 2 < -3.0 ? (default direction right)
tree[1].set_numerical_test_node(feature_id=2,
opname='<',
threshold=-3.0,
default_left=False,
left_child_key=3,
right_child_key=4)
# Node #3: leaf with output -0.4
tree[3].set_leaf_node(-0.4)
# Node #4: leaf with output +1.2
tree[4].set_leaf_node(1.2)
We must indicate which node is the root:
# Set node #0 as root
tree[0].set_root()
We are now done with the first tree. We insert it with the model builder
by calling append(). (Recall that the model
builder is really a list of tree objects, hence the method name append.)
# Insert the first tree into the ensemble
builder.append(tree)
The second tree is constructed analogously:
tree2 = treelite.ModelBuilder.Tree()
# Node #0: feature 1 < 2.5 ? (default direction right)
tree2[0].set_numerical_test_node(feature_id=1,
opname='<',
threshold=2.5,
default_left=False,
left_child_key=1,
right_child_key=2)
# Set node #0 as root
tree2[0].set_root()
# Node #1: leaf with output +1.6
tree2[1].set_leaf_node(1.6)
# Node #2: feature 2 < -1.2 ? (default direction left)
tree2[2].set_numerical_test_node(feature_id=2,
opname='<',
threshold=-1.2,
default_left=True,
left_child_key=3,
right_child_key=4)
# Node #3: leaf with output +0.1
tree2[3].set_leaf_node(0.1)
# Node #4: leaf with output -0.3
tree2[4].set_leaf_node(-0.3)
# Insert the second tree into the ensemble
builder.append(tree2)
We are now done building the member trees. The last step is to call
commit() to finalize the ensemble into
a Model object:
# Finalize and obtain Model object
model = builder.commit()
Note
Difference between ModelBuilder and
Model objects
Why does Treelite require one last step of “committing”? All
Model objects are immutable; once constructed,
they cannot be modified at all. So you won’t be able to add a tree or a node
to an existing Model object, for instance. On the other
hand, ModelBuilder objects are mutable, so that you
can iteratively build trees.
To ensure we got all details right, we can examine the resulting C program.
model.compile(dirpath='./test')
with open('./test/test.c', 'r') as f:
for line in f.readlines():
print(line, end='')
which produces the output
/* Other functions omitted for space consideration */
float predict_margin(union Entry* data) {
float sum = 0.0f;
if (!(data[0].missing != -1) || data[0].fvalue < 5) {
if ( (data[2].missing != -1) && data[2].fvalue < -3) {
sum += (float)-0.4;
} else {
sum += (float)1.2;
}
} else {
sum += (float)0.6;
}
if ( (data[1].missing != -1) && data[1].fvalue < 2.5) {
sum += (float)1.6;
} else {
if (!(data[2].missing != -1) || data[2].fvalue < -1.2) {
sum += (float)0.1;
} else {
sum += (float)-0.3;
}
}
return sum + (0);
}
The toy example has been helpful as an illustration, but it is impractical to manually specify nodes for real-world ensemble models. The following section will show us how to automate the tree building process. We will look at scikit-learn in particular.
Using the model builder to interface with scikit-learn¶
Scikit-learn (scikit-learn/scikit-learn) is a Python machine learning package known for its versatility and ease of use. It supports a wide variety of models and algorithms.
Treelite will be able to work with any decision tree ensemble models produced by scikit-learn. In particular, it will be able to work with
Note
Why scikit-learn? How about other packages?
We had to pick a specific example for programmatic tree construction, so we chose scikit-learn. If you’re using another package, don’t lose heart. As you read through the rest of section, notice how specific pieces of information about the tree ensemble model are being extracted. As long as your choice of package exposes equivalent information, you’ll be able to adapt the example to your needs.
Note
In a hurry? Try the sklearn module
The rest of this document explains in detail how to import scikit-learn
models using the builder class. If you prefer to skip all the gory details,
simply import the module treelite.sklearn.
import treelite.sklearn
model = treelite.sklearn.import_model(clf)
Note
Adaboost ensembles not yet supported
Treelite currently does not support weighting of member trees, so you won’t be able to use Adaboost ensembles.
Regression with RandomForestRegressor¶
Let’s start with the Boston house prices dataset, a regression problem. (Classification problems are somewhat trickier, so we’ll save them for later.)
We’ll be using RandomForestRegressor, a random
forest for regression. A random forest is an ensemble of decision trees
that are independently trained on random samples from the training data. See
this page for
more details. For now, just remember to specify random_forest=True in the
ModelBuilder constructor.
import sklearn.datasets
import sklearn.ensemble
# Load the Boston housing dataset
X, y = sklearn.datasets.load_boston(return_X_y=True)
# Train a random forest regressor with 10 trees
clf = sklearn.ensemble.RandomForestRegressor(n_estimators=10)
clf.fit(X, y)
We shall programmatically construct Tree
objects from internal attributes of the scikit-learn model. We only need
to define a few helper functions.
For the rest of sections, we’ll be diving into lots of details that are specific to scikit-learn. Many details have been adopted from this reference page.
The function process_model() takes in a scikit-learn ensemble object and
returns the completed Model object:
@classmethod
def process_model(cls, sklearn_model):
"""Process a RandomForestRegressor to convert it into a Treelite model"""
# Initialize Treelite model builder
# Set average_tree_output=True for random forests
builder = treelite.ModelBuilder(
num_feature=sklearn_model.n_features_, average_tree_output=True,
threshold_type='float64', leaf_output_type='float64')
# Iterate over individual trees
for i in range(sklearn_model.n_estimators):
# Process the i-th tree and add to the builder
# process_tree() to be defined later
builder.append(cls.process_tree(sklearn_model.estimators_[i].tree_,
sklearn_model))
return builder.commit()
The usage of this function is as follows:
from treelite.sklearn import SKLRFRegressorConverter
model = SKLRFRegressorConverter.process_model(clf)
We won’t have space here to discuss all internals of scikit-learn objects, but a few details should be noted:
The attribute
n_features_stores the number of features used anywhere in the tree ensemble.The attribute
n_estimatorsstores the number of member trees.The attribute
estimators_is an array of handles that store the individual member trees. To access the object for thei-th tree, writeestimators_[i].tree_. This object will be passed to the functionprocess_tree().
The function process_tree() takes in a single scikit-learn tree object
and returns an object of type Tree:
@classmethod
def process_tree(cls, sklearn_tree, sklearn_model):
"""Process a scikit-learn Tree object"""
treelite_tree = treelite.ModelBuilder.Tree(
threshold_type='float64', leaf_output_type='float64')
# Iterate over each node: node ID ranges from 0 to [node_count]-1
for node_id in range(sklearn_tree.node_count):
cls.process_node(treelite_tree, sklearn_tree, node_id, sklearn_model)
# Node #0 is always root for scikit-learn decision trees
treelite_tree[0].set_root()
return treelite_tree
Explanations:
The attribute
node_countstores the number of nodes in the decision tree.Each node in the tree has a unique ID ranging from 0 to
[node_count]-1.
The function process_node() determines whether each node is a leaf node
or a test node. It does so by looking at the attribute children_left:
If the left child of the node is set to -1, that node is thought to be
a leaf node.
@classmethod
def process_node(cls, treelite_tree, sklearn_tree, node_id, sklearn_model):
"""Process a tree node in a scikit-learn Tree object. Decide whether the node is
a leaf node or a test node."""
if sklearn_tree.children_left[node_id] == -1: # leaf node
cls.process_leaf_node(treelite_tree, sklearn_tree, node_id, sklearn_model)
else: # test node
cls.process_test_node(treelite_tree, sklearn_tree, node_id, sklearn_model)
The function process_test_node() extracts the content of a test node
and passes it to the Tree object that is
being constructed.
@classmethod
def process_test_node(cls, treelite_tree, sklearn_tree, node_id, sklearn_model):
# pylint: disable=W0613
"""Process a test node with a given node ID. We shall assume that all tree ensembles in
scikit-learn use only numerical splits."""
treelite_tree[node_id].set_numerical_test_node(
feature_id=sklearn_tree.feature[node_id],
opname='<=',
threshold=sklearn_tree.threshold[node_id],
threshold_type='float64',
default_left=True,
left_child_key=sklearn_tree.children_left[node_id],
right_child_key=sklearn_tree.children_right[node_id],)
Explanations:
The attribute
featureis the array containing feature indices used in test nodes.The attribute
thresholdis the array containing threshold values used in test nodes.All tests are in the form of
[feature value] <= [threshold].The attributes
children_leftandchildren_righttogether store children’s IDs for test nodes.
Note
Scikit-learn and missing data
Scikit-learn handles missing data differently than XGBoost and Treelite.
Before training an ensemble model, you’ll have to impute
missing values. For this reason, test nodes in scikit-learn tree models will
contain no “default direction.” We will assign default_left=True
arbitrarily for test nodes to keep Treelite happy.
The function process_leaf_node() defines a leaf node:
@classmethod
def process_leaf_node(cls, treelite_tree, sklearn_tree, node_id, sklearn_model):
# pylint: disable=W0613
"""Process a test node with a given node ID"""
# The `value` attribute stores the output for every leaf node.
leaf_value = sklearn_tree.value[node_id].squeeze()
# Initialize the leaf node with given node ID
treelite_tree[node_id].set_leaf_node(leaf_value, leaf_value_type='float64')
Let’s test it out:
from treelite.sklearn import SKLRFRegressorConverter
model = SKLRFRegressorConverter.process_model(clf)
model.export_lib(libpath='./libtest.dylib', toolchain='gcc', verbose=True)
import treelite_runtime
predictor = treelite_runtime.Predictor(libpath='./libtest.dylib')
predictor.predict(treelite_runtime.DMatrix(X))
Regression with GradientBoostingRegressor¶
Gradient boosting is an algorithm where decision trees are trained one at a
time, ensuring that latter trees complement former trees. See this page
for more details. Treelite makes distinction between random forests and
gradient boosted trees by the value of random_forest flag in the
ModelBuilder constructor.
Note
Set init='zero' to ensure compatibility
To make sure that the gradient boosted model is compatible with Treelite,
make sure to set init='zero' in the
GradientBoostingRegressor constructor. This
ensures that the compiled prediction subroutine will produce the correct
prediction output. Gradient boosting models trained without specifying
init='zero' in the constructor are NOT supported by Treelite!
# Gradient boosting regressor
# Notice the argument init='zero'
clf = sklearn.ensemble.GradientBoostingRegressor(n_estimators=10,
init='zero')
clf.fit(X, y)
We will recycle most of the helper code we wrote earlier. Only two functions will need to be modified:
@classmethod
def process_model(cls, sklearn_model):
"""Process a GradientBoostingRegressor to convert it into a Treelite model"""
# Check for init='zero'
if sklearn_model.init != 'zero':
raise treelite.TreeliteError("Gradient boosted trees must be trained with "
"the option init='zero'")
# Initialize Treelite model builder
# Set average_tree_output=False for gradient boosted trees
builder = treelite.ModelBuilder(
num_feature=sklearn_model.n_features_, average_tree_output=False,
threshold_type='float64', leaf_output_type='float64')
for i in range(sklearn_model.n_estimators):
# Process i-th tree and add to the builder
builder.append(cls.process_tree(sklearn_model.estimators_[i][0].tree_,
sklearn_model))
return builder.commit()
@classmethod
def process_leaf_node(cls, treelite_tree, sklearn_tree, node_id, sklearn_model):
"""Process a test node with a given node ID"""
leaf_value = sklearn_tree.value[node_id].squeeze()
# Need to shrink each leaf output by the learning rate
leaf_value *= sklearn_model.learning_rate
# Initialize the leaf node with given node ID
treelite_tree[node_id].set_leaf_node(leaf_value, leaf_value_type='float64')
Some details specific to GradientBoostingRegressor:
To indicate the use of gradient boosting (as opposed to random forests), we set
random_forest=Falsein theModelBuilderconstructor.Each tree object is now accessed with the expression
estimators_[i][0].tree_, asestimators_[i]returns an array consisting of a single tree (i-th tree).Each leaf output in gradient boosted trees are “unscaled”: it needs to be scaled by the learning rate.
Let’s test it:
from treelite.sklearn import SKLGBMRegressorConverter
# Convert to Treelite model
model = SKLGBMRegressorConverter.process_model(clf)
# Generate shared library
model.export_lib(libpath='./libtest2.dylib', toolchain='gcc', verbose=True)
# Make prediction with predictor
predictor = treelite_runtime.Predictor(libpath='./libtest2.dylib')
predictor.predict(treelite_runtime.DMatrix(X))
Binary Classification with RandomForestClassifier¶
For binary classification, let’s use the digits dataset. We will take 0’s and 1’s from the dataset and treat 0’s as the negative class and 1’s as the positive.
# load a binary classification problem
# Set n_class=2 to produce two classes
digits = sklearn.datasets.load_digits(n_class=2)
X, y = digits['data'], digits['target']
# Should print [0 1]
print(np.unique(y))
# Train a random forest classifier
clf = sklearn.ensemble.RandomForestClassifier(n_estimators=10)
clf.fit(X, y)
Random forest classifiers in scikit-learn store frequency counts for the positive and negative class. For instance, a leaf node may output a set of counts
[ 100, 200 ]
which indicates the following:
300 data points in the training set “belong” to this leaf node, in the sense that they all satisfy the precise sequence of conditions leading to that particular leaf node. The picture below shows that each leaf node represents a unique sequence of conditions:
100 of them are labeled negative; and
the remaining 200 are labeled positive.
Again, most of the helper functions may be re-used; only two functions need to be rewritten. Explanation will follow after the code:
@classmethod
def process_model(cls, sklearn_model):
"""Process a RandomForestClassifier (binary classifier) to convert it into a
Treelite model"""
builder = treelite.ModelBuilder(
num_feature=sklearn_model.n_features_, average_tree_output=True,
threshold_type='float64', leaf_output_type='float64')
for i in range(sklearn_model.n_estimators):
# Process i-th tree and add to the builder
builder.append(cls.process_tree(sklearn_model.estimators_[i].tree_,
sklearn_model))
return builder.commit()
@classmethod
def process_leaf_node(cls, treelite_tree, sklearn_tree, node_id, sklearn_model):
# pylint: disable=W0613
"""Process a test node with a given node ID"""
# Get counts for each label (+/-) at this leaf node
leaf_count = sklearn_tree.value[node_id].squeeze()
# Compute the fraction of positive data points at this leaf node
fraction_positive = float(leaf_count[1]) / leaf_count.sum()
# The fraction above is now the leaf output
treelite_tree[node_id].set_leaf_node(fraction_positive, leaf_value_type='float64')
As noted earlier, we access the frequency counts at each leaf node, reading the
value attribute of each tree. Then we compute the fraction of positive
data points with respect to all training data points belonging to the leaf.
This fraction then becomes the leaf output. This way, leaf nodes now produce
single numbers rather than frequency count arrays.
Why did we have to compute a fraction? For binary classification, Treelite expects each tree to produce a single number output. At prediction time, the outputs from the member trees will get averaged to produce the final prediction, which is also a single number. By setting the positive fraction as the leaf output, we ensure that the final prediction is a proper probability value. For instance, if an ensemble consisting of 5 trees produces the following set of outputs
Tree 0 0.1
Tree 1 0.7
Tree 2 0.4
Tree 3 0.3
Tree 4 0.7
then the final prediction will be 0.44, which we interpret as 44% probability for the positive class.
Multi-class Classification with RandomForestClassifier¶
Let’s use the digits dataset again, this time with 4 classes (i.e. 0’s, 1’s, 2’s, and 3’s).
# Load a multi-class classification problem
# Set n_class=4 to produce four classes
digits = sklearn.datasets.load_digits(n_class=4)
X, y = digits['data'], digits['target']
# Should print [0 1 2 3]
print(np.unique(y))
# Train a random forest classifier
clf = sklearn.ensemble.RandomForestClassifier(n_estimators=10)
clf.fit(X, y)
Random forest classifiers in scikit-learn store frequency counts (see the explanation in the previous section). For instance, a leaf node may output a set of counts
[ 100, 400, 300, 200 ]
which shows that the total of 1000 training data points belong to this leaf node and that 100, 400, 300, and 200 of them are labeled class 0, 1, 2, and 3, respectively.
We will have to re-write the process_leaf_node() function to accomodate multiple classes.
@classmethod
def process_model(cls, sklearn_model):
"""Process a RandomForestClassifier (multi-class classifier) to convert it into a
Treelite model"""
# Must specify num_class and pred_transform
builder = treelite.ModelBuilder(
num_feature=sklearn_model.n_features_, num_class=sklearn_model.n_classes_,
average_tree_output=True, pred_transform='identity_multiclass',
threshold_type='float64', leaf_output_type='float64')
for i in range(sklearn_model.n_estimators):
# Process i-th tree and add to the builder
builder.append(cls.process_tree(sklearn_model.estimators_[i].tree_,
sklearn_model))
return builder.commit()
@classmethod
def process_leaf_node(cls, treelite_tree, sklearn_tree, node_id, sklearn_model):
# pylint: disable=W0613
"""Process a test node with a given node ID"""
# Get counts for each label class at this leaf node
leaf_count = sklearn_tree.value[node_id].squeeze()
# Compute the probability distribution over label classes
prob_distribution = leaf_count / leaf_count.sum()
# The leaf output is the probability distribution
treelite_tree[node_id].set_leaf_node(prob_distribution, leaf_value_type='float64')
The process_leaf_node() function is quite similar to what we had for the
binary classification case. Only difference is that, instead of computing the
fraction of the positive class, we compute the probability distribution for
all possible classes. Each leaf node thus will store the probability
distribution of possible class outcomes.
The process_model() function is also similar to what we had before. The
crucial difference is the existence of parameters num_class and
pred_transform. The num_class parameter is used only for
multi-class classification: it should store the number of classes (in this
example, 4). The pred_transform parameter should be set to
'identity_multiclass', to indicate
that the prediction should be made simply by averaging the probability
distribution produced by each leaf node. (Leaf outputs are averaged rather
than summed because we set random_forest=True.) For instance, if an ensemble
consisting of 3 trees produces the following set of outputs
Tree 0 [ 0.5, 0.5, 0.0, 0.0 ]
Tree 1 [ 0.1, 0.5, 0.3, 0.1 ]
Tree 2 [ 0.2, 0.5, 0.2, 0.1 ]
then the final prediction will be the average
[ 0.26666667, 0.5, 0.16666667, 0.06666667 ], which indicates 26.7%
probability for the first class, 50.0% for the second, 16.7% for the third,
and 6.7% for the fourth.
Binary Classification with GradientBoostingClassifier¶
We use the digits dataset. We will take 0’s and 1’s from the dataset and treat 0’s as the negative class and 1’s as the positive.
# Load a binary classification problem
# Set n_class=2 to produce two classes
digits = sklearn.datasets.load_digits(n_class=2)
X, y = digits['data'], digits['target']
# Should print [0 1]
print(np.unique(y))
# Train a gradient boosting classifier
# Notice the argument init='zero'
clf = sklearn.ensemble.GradientBoostingClassifier(n_estimators=10,
init='zero')
clf.fit(X, y)
Note
Set init='zero' to ensure compatibility
To make sure that the gradient boosted model is compatible with Treelite,
make sure to set init='zero' in the
GradientBoostingClassifier constructor. This
ensures that the compiled prediction subroutine will produce the correct
prediction output. Gradient boosting models trained without specifying
init='zero' in the constructor are NOT supported by Treelite!
Here are the functions process_model() and process_leaf_node() for this
scenario:
@classmethod
def process_model(cls, sklearn_model):
"""Process a GradientBoostingClassifier (binary classifier) to convert it into a
Treelite model"""
# Check for init='zero'
if sklearn_model.init != 'zero':
raise treelite.TreeliteError("Gradient boosted trees must be trained with "
"the option init='zero'")
# Initialize Treelite model builder
# Set average_tree_output=False for gradient boosted trees
# Set pred_transform='sigmoid' to obtain probability predictions
builder = treelite.ModelBuilder(
num_feature=sklearn_model.n_features_, average_tree_output=False,
pred_transform='sigmoid', threshold_type='float64', leaf_output_type='float64')
for i in range(sklearn_model.n_estimators):
# Process i-th tree and add to the builder
builder.append(cls.process_tree(sklearn_model.estimators_[i][0].tree_,
sklearn_model))
return builder.commit()
@classmethod
def process_leaf_node(cls, treelite_tree, sklearn_tree, node_id, sklearn_model):
"""Process a test node with a given node ID"""
leaf_value = sklearn_tree.value[node_id].squeeze()
# Need to shrink each leaf output by the learning rate
leaf_value *= sklearn_model.learning_rate
# Initialize the leaf node with given node ID
treelite_tree[node_id].set_leaf_node(leaf_value, leaf_value_type='float64')
Some details specific to GradientBoostingClassifier:
To indicate the use of gradient boosting (as opposed to random forests), we set
random_forest=Falsein theModelBuilderconstructor.Each tree object is now accessed with the expression
estimators_[i][0].tree_, asestimators_[i]returns an array consisting of a single tree (i-th tree).Each leaf output in gradient boosted trees are “unscaled”: it needs to be scaled by the learning rate.
In addition, we specify the parameter pred_transform='sigmoid' so that
the final prediction yields the probability for the positive class. For example,
suppose that an ensemble consisting of 4 trees produces the following set of
outputs:
Tree 0 +0.5
Tree 1 -2.3
Tree 2 +1.5
Tree 3 -1.5
Unlike the random forest example earlier, we do not assume that each leaf output is between 0 and 1; it can be any real number, negative or positive. These numbers are referred to as margin scores, to distinguish them from probabilities.
To obtain the probability for the positive class, we first sum the margin scores (outputs) from the member trees.
Tree 0 +0.5
Tree 1 -2.3
Tree 2 +1.5
Tree 3 -1.5
--------------
Total -1.8
Then we apply the sigmoid function:
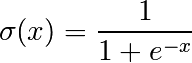
The resulting value is the final prediction. You may interpret this value as a probability. For the particular example, the sigmoid value of -1.8 is 0.14185106, which we interpret as 14.2% probability for the positive class.
Multi-class Classification with GradientBoostingClassifier¶
Let’s use the digits dataset again, this time with 4 classes (i.e. 0’s, 1’s, 2’s, and 3’s).
# Load a multi-class classification problem
# Set n_class=4 to produce four classes
digits = sklearn.datasets.load_digits(n_class=4)
X, y = digits['data'], digits['target']
# Should print [0 1 2 3]
print(np.unique(y))
# Train a gradient boosting classifier
# Notice the argument init='zero'
clf = sklearn.ensemble.GradientBoostingClassifier(n_estimators=10,
init='zero')
clf = sklearn.ensemble.RandomForestClassifier(n_estimators=10)
clf.fit(X, y)
Note
Set init='zero' to ensure compatibility
To make sure that the gradient boosted model is compatible with Treelite,
make sure to set init='zero' in the
GradientBoostingClassifier constructor. This
ensures that the compiled prediction subroutine will produce the correct
prediction output. Gradient boosting models trained without specifying
init='zero' in the constructor are NOT supported by Treelite!
Here are the functions process_model() and process_leaf_node() for this
scenario:
@classmethod
def process_model(cls, sklearn_model):
"""Process a GradientBoostingClassifier (multi-class classifier) to convert it into a
Treelite model"""
# Check for init='zero'
if sklearn_model.init != 'zero':
raise treelite.TreeliteError("Gradient boosted trees must be trained with "
"the option init='zero'")
# Initialize Treelite model builder
# Set average_tree_output=False for gradient boosted trees
# Set num_class for multi-class classification
# Set pred_transform='softmax' to obtain probability predictions
builder = treelite.ModelBuilder(
num_feature=sklearn_model.n_features_, num_class=sklearn_model.n_classes_,
average_tree_output=False, pred_transform='softmax',
threshold_type='float64', leaf_output_type='float64')
# Process [number of iterations] * [number of classes] trees
for i in range(sklearn_model.n_estimators):
for k in range(sklearn_model.n_classes_):
builder.append(cls.process_tree(sklearn_model.estimators_[i][k].tree_,
sklearn_model))
return builder.commit()
@classmethod
def process_leaf_node(cls, treelite_tree, sklearn_tree, node_id, sklearn_model):
"""Process a test node with a given node ID"""
leaf_value = sklearn_tree.value[node_id].squeeze()
# Need to shrink each leaf output by the learning rate
leaf_value *= sklearn_model.learning_rate
# Initialize the leaf node with given node ID
treelite_tree[node_id].set_leaf_node(leaf_value, leaf_value_type='float64')
The process_leaf_node() function is identical to one in the previous
section: as before, each leaf node produces a single real-number output.
On the other hand, the process_model() function needs some explanation.
First of all, the attribute estimators_ of the scikit-learn model object
now stores output groups, which are simply groups of decision trees.
The expression estimators_[i] thus refers to the i th output group.
Each output group contains as many trees as there are label classes. For the
digits example with 4 label classes, we’d have 4 trees for each output group:
estimators_[i][0], estimators_[i][1], estimators_[i][2], and
estimators_[i][3]. Since there are as many output groups as the number of
iterations used for training, the total number of member trees is
[number of iterations] * [number of classes]. We have to call append()
once for each member tree; hence the use of nested loop.
We also set pred_transform='softmax', which indicates the way margin
outputs should be transformed to produce probability predictions. Let us look
at a concrete example: suppose we train an ensemble model with 3 rounds of
gradient boosting. It would produce a total of 12 decision trees (3 rounds *
4 classes). Suppose also that, given a single test data point, the model
produces the following set of margins:
Output group 0:
Tree 0 produces +0.5
Tree 1 produces +1.5
Tree 2 produces -2.3
Tree 3 produces -1.5
Output group 1:
Tree 4 produces +0.1
Tree 5 produces +0.7
Tree 6 produces +1.5
Tree 7 produces -0.9
Output group 2:
Tree 8 produces -0.1
Tree 9 produces +0.3
Tree 10 produces -0.7
Tree 11 produces +0.2
How do we compute probabilities for each of the 4 classes? First, we compute the sum of the margin scores for each output group:
Output group 0:
Tree 0 produces +0.5
Tree 1 produces +1.5
Tree 2 produces -2.3
Tree 3 produces -1.5
----------------------
SUBTOTAL -1.8
Output group 1:
Tree 4 produces +0.1
Tree 5 produces +0.7
Tree 6 produces +1.5
Tree 7 produces -0.9
----------------------
SUBTOTAL +1.4
Output group 2:
Tree 8 produces -0.1
Tree 9 produces +0.3
Tree 10 produces -0.7
Tree 11 produces +0.2
----------------------
SUBTOTAL -0.3
The vector [-1.8, +1.4, -0.3] consisting of the subtotals quantifies the
relative likelihood of the label classes. Since the second element (1.4) is
the largest, the second class must be the most likely outcome for the particular
data point. This vector is not yet a probability distribution, since its
elements do not sum to 1.
The softmax function transforms any real-valued vector into a probability distribution as follows:
Apply the exponential function (
exp) to every element in the vector. This step ensures that every element is positive.Divide every element by the sum over the vector. This step is also known as normalizing the vector. After thie step, the elements of the vector will add up to 1.
Let’s walk through the steps with the vector [-1.8, +1.4, -0.3]. Applying
the exponential function is simple with Python:
x = np.exp([-1.8, +1.4, -0.3])
print(x)
which yields
[ 0.16529889 4.05519997 0.74081822]
Note that every element is now positive. Then we normalize the vector by writing
x = x / x.sum()
print(x)
which gives a proper probability distribution:
[ 0.03331754 0.8173636 0.14931886]
We can now interpret the result as giving 3.3% probability for the first class, 81.7% probability for the second, and 14.9% probability for the third.